رایانه‌ها را می‌توان به عنوان ابزارهای با ارزشی معرفی کرد که ریاضیدان‌ها را در مسیر حل یک مساله ریاضی یاری می‌کنند، اما این ابزار‌ها که روز به روز نیز هوشمند‌تر می‌شوند، می‌توانند نقش بزرگ‌تری را برای کشف و اثبات یک قضیه‌ی ریاضی بر عهده گیرند.

استفاده از رایانه‌ها برای اثبات مسائل ریاضی سابقه‌ای بیش از ۴۰ سال دارد. اولین مساله‌ای که در آن از رایانه برای اثبات کمک گرفته شده، قضیه‌ی چهار رنگ است. براساس قضیه‌ی چهار رنگ برای رنگ آمیزی یک نقشه تنها وجود چهار رنگ کافی است و برای مثال در مورد نقشه‌ی کشورها، می‌توان به تمام کشور یک رنگ اختصاص داد، بدون اینکه دو کشور با رنگ یکسان در کنار هم قرار گیرند.

اثبات این قضیه برای اولین بار در سال ۱۹۷۶ میلادی با استفاده از رایانه ارائه شده، اما بعدها مشکلاتی در اثبات مورد نظر پیدا شد و اثبات صحیح این مساله تا سال ۱۹۹۵ تکمیل شد.

در سال ۲۰۰۳، توماس هیلز از دانشگاه پیتسبورگ اثباتی را برای قضیه‌ی کپلر که در آن از یاری رایانه‌ها کمک گرفته شده بود، منتشر کرد. قضیه یا حدس کپلر در پی آن است تا بهینه‌ترین حالت ممکن برای قرار گرفتن تعداد حداکثری اشیا با فرم کره را در یک فضای اقلیدسی ارائه کند. قضیه کپلر به زبان ساده بهینه‌ترین روش چیدن پرتقال روی یکدیگر به گونه‌ای است که در میوه فروشی‌ها چیده می‌شود.

اگرچه توماس هیلز اثبات خود را در سال ۲۰۰۳ میلادی منتشر کرد، اما بسیاری از ریاضیدان‌ها این اثبات را به دلیل حجم بالای آن و سخت بودن فرآیند صحیح بودن اثبات انجام شده، قبول نکردند، چراکه حجم اثباتی که هیلز با استفاده از رایانه به آن دست یافته بود، بیش از ۲ گیگابایت بود که در زمان خود حافظه‌ی بسیار زیادی به شمار می‌رفت. اما هیلز ناامید نشده و با استفاده از یک اثبات تصدیق شده که با استفاده از رایانه به دست آمده بود، موفق به اثبات قضیه کپلر شد.

قضیه سه گانه پولی فیثاغورس، آخرین مساله اثبات شده با استفاده از ابررایانه

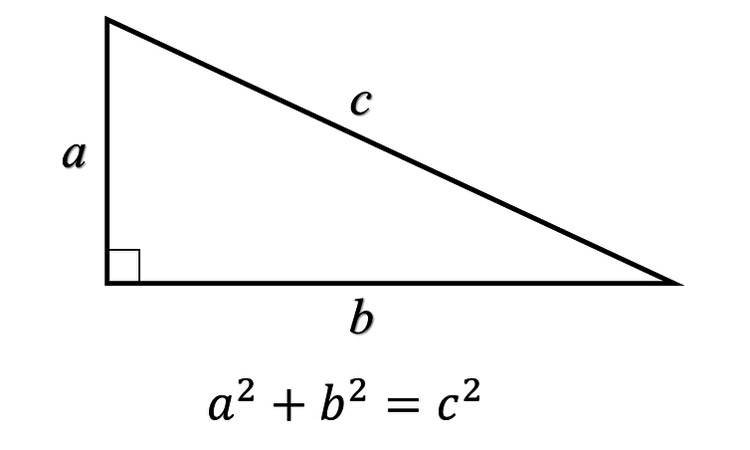
از جمله‌ی آخرین اثبات‌هایی که برای یک مساله‌ی ریاضی ارائه شده، مربوط به قضیه سه گانه بولی فیثاغورس است. اثبات ارائه شده نشان می‌دهد که می‌توان اعداد یک تا ۷٫۸۲۴ را به گونه‌ای با استفاده از رنگ‌های آبی و قرمز رنگ‌آمیزی کرد که هیچ یک از سه عددی که در معادله‌ی a2 + b2 = c2 قرار می‌گیرند، دارای رنگ یکسانی نباشند. در واقع ابتدا باید تمام اعدادی را که در این معادله قرار گرفته و تساوی برقرار می‌شود را یافته و سپس آن‌ها را طوری رنگ‌آمیزی کرد که در ترکیب با اعداد دیگر نیز شاهد همرنگ بودن سه عدد مورد نظر نباشیم. برای مثال سه عدد ۵، ۱۲ و ۱۳ را می‌توان به عنوان b، a و c در معادله قرار داد، حال آنکه اعداد ۳، ۴ و ۵ نیز به ترتیب بالا در معادله فیثاغورس قرار گرفته و تساوی را برقرار می‌کنند. با توجه به اینکه عدد ۵ در هر دو ترکیب نیز وجود دارد، پس باید رنگ هر یک از اعداد به گونه‌ای انتخاب شود تا در صورت حضور در ترکیب اعداد دیگری که تساوی را برقرار می‌کنند نیز شاهد حضور رنگ‌های متفاوت باشیم.

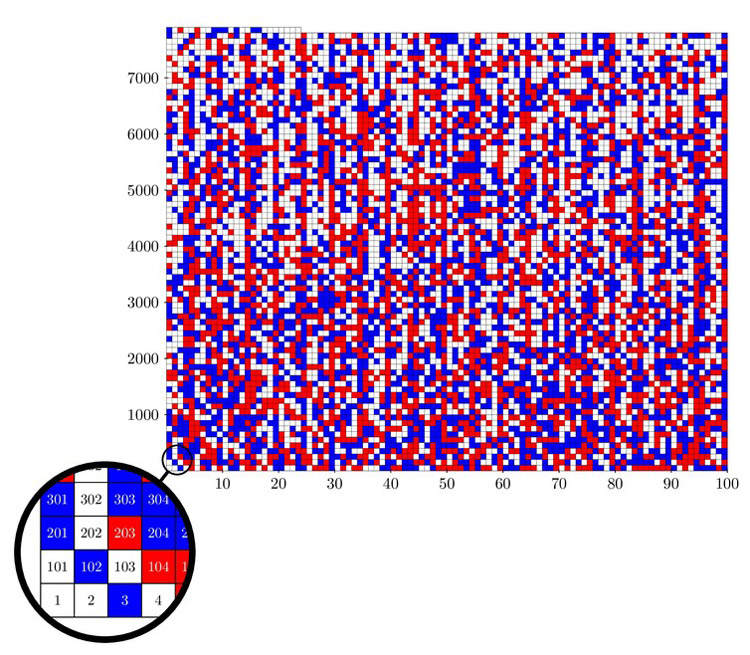
دانشمندان با استفاده از علم احتمال، مجموعه‌ی حالاتی را که اعداد یک تا ۷٫۸۲۵ می‌توانند رنگ متفاوتی به خود بگیرند را 102,300 حالت بیان کرده‌اند. این عدد از تعداد ذرات بنیادی که تاکنون در جهان هستی کشف شده نیز بیشتر است.

البته دانشمندان موفق شده‌اند تا با استفاده از روش‌‌های تقارن و تئوری اعداد، تعداد احتمالات موجود را به کمتر از یک تریلیون حالت کاهش دهند. برای آزمایش هر یک از حالات مورد نظر با استفاده از ابررایانه‌ی Stampede متعلق به دانشگاه تگزاس که از وجود بیش از ۸۰۰ هسته پردازشی بهره می‌برد، یک روز زمان نیاز است. ابررایانه‌ی مورد نظر قادر است تا 1019 ریاضی را به انجام برساند.

شبکه‌‌ی بزرگی از رایانه‌ها در سطح جهان که با نام GIMPS (Great Internet Mersenne Prime Search) شناخته می‌شود، قادر است در هر ثانیه بیش از ۴۵۰ تریلیون عملیات ریاضی را انجام دهد. از این شبکه‌ی رایانه‌ای برای پیدا کردن بزرگ‌ترین عدد اول استفاده می‌شود. این شبکه‌ی رایانه‌ای قادر است پس از ۶ ساعت فعالیت به توان ابررایانه‌ی تگزاس برسد.

این ابررایانه پس از انجام پردازش و تحلیل هر یک از حالت‌های خود، اثبات خود را با حجم ۲۰۰ ترابایت ارائه کرد که با تقسیم آن به هر یک از انسان‌های موجود روی زمین، به هر نفر ۳۰٫۰۰۰ بایت اطلاعات می‌رسد.

آیا دوره ریاضیدانان به پایان رسیده است؟

پیشرفت‌های حاصل شده در دنیای فناوری به چه معنا است؟ آیا در آینده‌ی نزدیک باید ریاضیدانان را نیز همچون رانندگان تاکسی، فروشندگان کالا، رادیولوژیست‌ها و سایر شغل‌هایی که ماهیتی نسبتا تکراری دارند، دچار روزمرگی و از بین رفتن بدانیم؟

به طور قطع پاسخ این سوال منفی است. ریاضیدان‌ها همچون بسیاری از حرفه‌های دیگر، بهره‌گیری از رایانه‌ها را به عنوان روش جدیدی از انجام تحقیقات مورد استفاده قرار می‌دهند، بطوریکه که فرآیند جدید استفاده از رایانه‌ها باعث تولید شاخه‌ی جدیدی از این رشته با عنوان ریاضیات تجربی شده است که مزایا و نتایج آن بسیار گسترده است.

اما ریاضیات تجربی به چه معنا است؟ بهترین تعریف برای ریاضیات تجربی را می‌توان به کار گرفتن رایانه‌ها به عنوان آزمایشگاهی برای تحقیقات عنوان کرد. برای مثال در رشته‌ها نظیر شیمی، فیزکی، زیست شناسی و مهندسی نیز برای انجام آزمایش‌ها و مدلسازی از وجود رایانه‌ها استفاده کرده و فرضیه‌های خود را با استفاده از این ابزار و براساس راه‌های مشخص و مرسوم اثبات می‌کنند.

البته از یک نظر ریاضیات تجربی مفهوم چندان جدیدی بصورت بنیادی نیست. دانشمند بزرگ یونانی، ارشمیدس در قرن سوم پیش از میلاد در این خصوص چنین اظهار نظر کرده است:

ریاضیات تجربی مبتنی بر فناوری‌های رایانه‌ای در کنار خود تکنولوژی را به خدمت گرفته‌اند. با گذشت هر سال و تقویت بیش از پیش قدرت سخت‌افزاری رایانه‌های مورد استفاده بسیاری از نرم‌افزار‌های مورد استفاده برای انجام محاسبات ریاضی نظیر Maple، Mathematica، Saga و سایر گزینه‌های موجود بیش از پیش تقویت می‌شوند.

هرچند استفاده و وجود اثبات‌های مبتنی بر دانش انسانی ضروری به نظر می‌رسد، اما رایانه‌ها نیز برای یاری ریاضیدانان به منظور اثبات تئوری‌های جدید و ارائه‌ی استنتاج قوی، در حال پیشرفت و در دست گرفتن امور هستند.

البته در مقام مقایسه، اثبات‌های ارائه شده توسط رایانه‌ها بسیار متقاعد کننده و صحیح هستند، چراکه انسان به دلیل برخورداری از ذاتی خطاپذیر، بعضا اثبات‌هایی را ارائه کرده که دچار مشکلاتی بوده‌ و خواهند بود، هرچند در رایانه‌ها به دلیل اینکه ماشین از قوانین خاصی پیروی می‌کند، امکان بروز خطا به خودی خود ممکن نیست.

برای مثال می‌توان به پیدا کردن بزرگ‌ترین اعشار عدد پی اشاره کرد که توسط آلکساندر یی و شیجرو کوندو انجام شده و تا ۱۲.۱ تریلیون رقم از عدد پی را پیدا کرده‌اند. این دو دانشمند پس از پایان یافتن عملیات، بخشی از محاسبات خود را با یک الکوریتم دیگر که به صورت کامل متفاوت بود، انجام دادند و پس از آنکه مشخص شد نتایج به دست آمده با نتیجه‌ی روش اول در موارد آزمایش یکی است پی به صحیح بودن روش مورد استفاده بردند.

آینده در این مورد چه می‌گوید؟

با پیشرفت علوم رایانه‌ای و ترکیب هر چه بیشتر آن با تحلیل‌های ریاضی دانشمندان، ریاضیدانان برای سپردن بخشی از فرآیند اثبات مسائل ریاضی مشکل نداشته و پروسه اثبات مسائل بسیار راحت‌تر از پیش خواهد شد.

دانشمندان بلند پایه‌ی دنیای ریاضی معتقدند که با وجود پیشرفت روزافزون اثبات‌های ریاضی در سال‌های آینده، همچنان بخش زیادی از این فرآیند توسط دانشمندان و متخصصان ریاضی انجام خواهد شد.